课 题:数系的扩充与复数的概念
教学目标
1、了解引进复数的必要性;理解虚数单位i以及i与实数的四则运算规律.理解并掌握复数的有关概念(复数集、代数形式、虚数、纯虚数、实部、虚部)
2、 由经历解方程的运作领悟引入复数的必要性,在探索复数有关概念中进一步提升合作、交流水平,在定义复数相等的探讨中增强数学转化意识.
3、在问题情境中了解数系的扩充过程,体会实际需求与数学内部矛盾( 数的运算规则、方程求根) 在数系扩充过程中的作用,感受人类理性思维的作用,以及数与现实世界的联系.
教学重点:复数的概念,虚数单位i,复数的分类(实数、虚数、纯虚数)等概念
教学难点:虚数与纯虚数的区别,复数的概念
教学方法:先学后讲,探究启发式
课 时:1课时
教学过程:
第一站:忆方程, 回首数系发展, 了然于胸
1、请大家说出方程x -1 =0 的解.
有学生介绍自然数的历史:人类历史上最早产生的数是自然数, 早在人类社会初期, 人们在狩猎、采集果实等劳动中, 由于计数的需要, 就产生了1 , 2 , 3 , 4 , …以及表示“没有”的0 , 于是就产生了自然数.
2、说出方程(x-1)(x +1)=0 的解.
学生介绍复数的数学史学生:值得我们骄傲的是我国是首先使用负数的国家.世界上第一部关于负数完整介绍的古算书是《九章算术》.公元前3 世纪刘徽在注解《九章算术》时率先给出了负数的定义:“两算得矢相反, 要以正负以名之” , 并辩证地阐明:“言负者未必少, 言正者未必正于多.” 而西方直到1572 年, 意大利数学家邦贝利在他的《代数学》中才给出了负数的明确定义.
3、说出方程(x-1)(x +1)(2x -1)=0 的解.
学生介绍分数的历史:人类在度量和均分时往往不能正好得到整数的结果, 这样就产生了分数.无论是分数确切定义和科学表示, 还是分数的算法, 最早建立起来的都是中国.《九章算术》中就已经有约分、通分以及分数的四则运算等知识.
4、说出方程(x-1)(x +1)(2 x -1)(x2 -2)=0 的解.
幻灯片(学生结合幻灯片作简单介绍):…… 希帕索斯说:“ … …我演算了很多次, 任何等腰直角三角形的直角边无法去量准斜边, 都不能用一个精确的数字表示出来.”这话像一声晴天霹雳, 立即响起一阵怒吼:“你敢违背毕达哥拉斯先生的理论, 敢破坏我们学派的信条!” … …希帕索斯抗议着:“你们无视科学, 你们竟这样无理!” … …毕氏门徒就把希帕索斯扔进了海里.蓝色的海水很快淹没了他的躯体,再也没有出来.希帕索斯为捍卫真理付出了沉重的代价.
问:刚才我们回顾了已经学过的数系发展的历史(幻灯片显示数系发展顺序), 请大家表示出我们已经学过的数系之间的包含关系.学生在学案上表示出, 教师巡视检查.
5、下面请看方程(x -1)(x +1)(2 x -1)(x2 -2)(x2 +1)=0 的解, 我们知道在不同的数系范围内, 这个方程的解是不同的, 那么方程x2 +1 =0 有解吗?
6、思考:为什么方程x2 +1 =0 没有实数解?
第二站:制高点, 鸟瞰虚数复数, 拨云见日
1、扩充数系
(1)引入i 表示虚数单位, 并且规定i2 =-1 .
(2)介绍公式“eiπ+1=0” .
规定:(1)i2 =-1 ;意大利数学家邦贝利给出了虚数单位与实数的四则运算;(2)实数可以与i 进行四则运算, 在进行四则运算时, 原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立.
2、人在旅途, 同伴互助
请大家给出虚数单位i 与实数3 进行四则运算的式子.
教师请一位学生将他的成果进行展示:3+i , i+3 , 3-i , i-3 ,3i , i/3 , 3/i .
问:请仔细观察, 这些数从形式上看都有什么共同特点? 你能归纳出它的一般形式吗?
预设:大家对数3/i感到困惑.(提示:回忆对3/ 进行化简的过程:分母有理化.类比化简3/i )
进行化简的过程:分母有理化.类比化简3/i )
3、复数的概念
形如 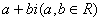 的数,我们把它们叫做复数,其中
的数,我们把它们叫做复数,其中 叫做复数的实部,
叫做复数的实部,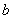 叫做复数的虚部。
叫做复数的虚部。
注意:
(1)“复数”非“负数”
(2)全体复数形成的集合叫做复数集,用大写字母C表示。
(3)德国著名数学家高斯首先给出了复数的概念, 高斯在数学界享有盛誉, 被称为“数学王子”.
4、例题分析
例1 :请说出下列复数的实部与虚部.
问:请观察这些复数实部与虚部的特点, 你能从某种角度对复数进行适当的分类吗?
学生相互讨论, 最后给出初步结论:可以根据实部或虚部是否为零进行分类.
5、复数的分类
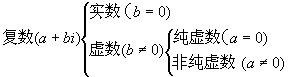
教师继续引导学生对数系进行扩充.
例2: 当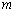 取何实数时,复数
取何实数时,复数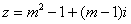 是:
是:
(1)实数 (2) 虚数 (3)纯虚数
解后反思:总结解决问题的过程中用到了哪些数学思想?
提示:分类、方程、化归
第三站:塑理性, 回顾真理之路, 勇往直前
1、说出方程方程x2+1 =0的解。
2、教师介绍复数的发展历史,
3、旅途回望
请大家谈谈我们这堂课学习了哪些知识? 运用了哪些思想? 又有哪些体验和感悟呢?
4、数之旅休息站
教师布置课后拓展作业:
(1)请阅读书籍《虚数的故事》.
(2) 登录网站http ://w w w .mat rix67 .com/blog/archives/tag/ %E8 %99 %9A %E6 %95 %查阅有关虚数的资料.
(3)做好继续“数之旅”的复习与预习工作.